Pinterest OA – Implement Naive Bayes Classifier (Machine Learning Coding Assessment)

Question 1

You are asked to implement parts of a Naive Bayes classification algorithm from scratch, without using any libraries except numpy and math. Naive Bayes classification is based on Bayes’Theorem, predicting the probability that a set of data points belongs to one of several classes.

A full Naive Bayes classifier consists of four major steps:

1. Calculate feature statistics by class
   Compute the mean and variance of each feature in x_train for each class label in y_train.
2. Calculate prior probabilities
   Calculate the proportion of training samples belonging to each class.
3. Implement the Gaussian Density Function The density function is: f(x) = 1/(σ√(2π)) * exp(- (x - μ)² / (2σ²) ) where μ is the mean and σ is the standard deviation of the feature.

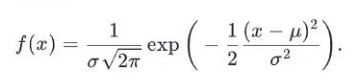
• Calculate posterior probabilities and make predictions
  Using Bayes’Theorem: ŷ = argmax_k P(C_k) * Π f(xi | C_k) where C_k is a class label.

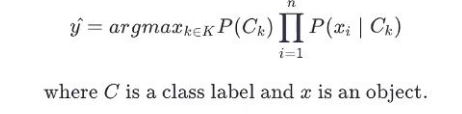
You are given:

• x_train: 2D array of float values
• y_train: 1D array of class labels
• x_test: 2D array of float values (same format as train data, without labels)

Your task is to implement only the missing sections under # implement this.

Input

x_train = [[-2.6, 1.9, 2.0, 1.0],[-2.8, 1.7, -1.2, 1.5],[2.0, -0.9, 0.3, 2.3],[-1.5, -0.1, -1.6, -1.1],[-1.0, -0.6, -1.2, -0.7],[-0.3, 1.2, 2.6, 0.2],[-1.8, -1.3, -0.1, -1.2],[0.2, 1.2, -0.6, -1.3],[-5.2, 3.0, 0.2, 2.2],[-0.8, -0.1, 1.5, -0.1],[-2.3, 3.0, 0.8, 0.7],[0.2, 3.0, 3.6, -0.9],[1.7, -0.8, -0.0, 2.0],[2.8, 0.8, 1.8, -0.7]] y_train = [1, 2, 0, 0, 0, 1, 0, 1, 2, 0, 2, 1, 0, 2] x_test = [[-0.1, 1.4, 0.4, -1.0],[-1.3, 0.2, -1.3, -0.8],[-1.1, 1.5, -2.3, -2.5]]

Output

solution(x_train, y_train, x_test) = [1, 0, 1]

Question 2

Implement the missing code, denoted by ellipses. You may not modify the pre-existing code.

Your task is to implement parts of the Bagging algorithm from scratch (i.e., without importing any external libraries besides those already imported). As a reminder, Bagging classification comprises three major steps:

1. Bootstrap the train samples for each base classifier.
2. Train each classifier based on its own bootstrapped samples.
3. Assign class labels by a majority vote of the base classifiers.

To validate your implementation, you will use it for some classification tasks. Specifically, you will be given:

• x_train: a two-dimensional array of float values, where each subarray x_train[i] represents a unique case.
• y_train: a one-dimensional array where each element is the true class label of the corresponding x_train[i].
• x_test: test data in the same format as the training data but without labels.
• n_estimators: the number of base classifiers.

Your model should fit the training data, then classify each sample in x_test, and return the predicted class labels.

Notes

• All training/test data will be float values.
• Do not modify any pre-existing code—only fill in the # implement this parts.
• In a tie, choose the class label with the smaller number.
• Bootstrapping rules:
  • Generate indices using randint(0, n) where n is the number of training samples.
  • Indices may repeat by nature of bootstrapping.
  • seed is used only initially.

Question 3

You are given a string expr representing a sum of two positive integers. Both integers do not contain zeros in their decimal representation. For example, expr can contain "741+12" — but it cannot be equal to "74112" or "740+12".

You must add exactly one pair of parentheses to expr so that:

1. The plus sign '+' is inside the parentheses.
2. There is at least one digit before the plus sign and at least one digit after it.

For example:
"741+12" may be transformed into:

• "7(41+1)2"
• "74(1+12)"

But it cannot be turned into:

• "(74)1+12"
• "74(1)+12"

The resulting string must still represent a valid arithmetic expression.

You must compute the minimum possible value obtained after placing the parentheses.

Example:

For expr = "112+422",
all possible evaluated cases include:

(112+422) = 534  (11(2+4)22) = 308  (112+4)22 = 2552  1(12+422) = 434  1(12+4)22 = 108  ← smallest  ...

The output should be:

solution(expr) = 108

The VOprep team has long accompanied candidates through various major company OAs and VOs, including Coinbase, Google, Amazon, Citadel, SIG, providing real-time voice assistance, remote practice, and interview pacing reminders to help you stay smooth during critical moments. If you are preparing for these companies, you can check out our customized support plans—from coding interviews to system design, we offer full guidance to help you succeed.